My work

Developing new methods to deal with the CMB polarized foregrounds.

The moment expansion: generalities

My main research interest is to develop and test innovative methods in order to face the foreground challenge in the quest of the primordial $B$-modes with present and future CMB missions. My primary focus in the past years was to investigate the so-called moment expansion method proposed by Chluba et al (2017). This method was developed to treat the distortions of the foreground signal coming from averaging effects. Indeed, the physical conditions (temperature, composition …) are varying across our Galaxy and hence across the sky. As such, any astrophysical observation presents itself as a mixture of emission points associated with different properties, phenomenon known as “mixing”. Due to the non-linearity of the spectral energy distributions (SED) of the astrophysical sources, the averaged signal does not behave as the local one: the total SED is said to be “distorted”. The moment expansion propose to perform a Taylor expansion of the local SED $I_\nu^{\rm loc}$ with respect to its spectral parameters $p=(p_1,p_2…)$ around common pivots $\bar{p}=(\bar{p_1},\bar{p_2}, …)$ in order to express the total distorted SED $I^{\rm tot}_\nu$ as

\[I^{\rm tot}_\nu= I^{\rm loc}_\nu(\bar{p})\left(1+ \sum_i\omega^{p_i}_1\frac{\partial I^{\rm loc}_\nu}{\partial p_i} + \frac{1}{2}\sum_{i,j}\omega^{p_ip_j}_2\frac{\partial^2 I^{\rm loc}_\nu}{\partial p_i\partial p_j} + \cdots \right)\]

The coefficients $\omega_i^{p}$ of this expansion are called the “moments” and are directly related to the statistical moments of the distributions of the spectral parameters $p$ that one is averaging over. As such, measuring the value of the moments can allow us to infer the properties of the Galactic signal. As desired, each term of the expansion models finer and finer distortions effects and thus allow to account for the complexity of the foreground signal in a minimal and well motivated way.

Application of the moment expansion for component separation

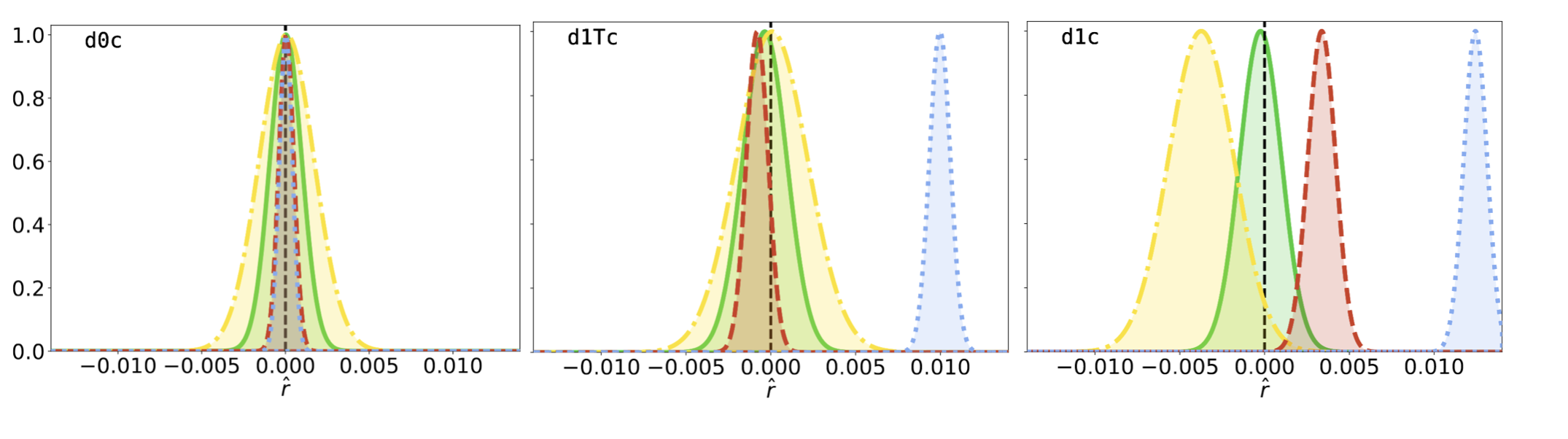
Recovered posterior distribution for the tensor-to-scalar ratio $\hat{r}$ with increasing complexity of the dust signal and moment expansion at different orders used to model the signal (for explanations see Vacher et al (2022))

The moment expansion formalism was generalized at the angular power spectra level to analyse the Planck data in Mangilli et al (2021). In my first work, Vacher et al (2022), I re-used and extended this formalism to perform component separation with simulated LiteBIRD data. I demonstrated that – at least in simple cases – the moment expansion provided a viable way to clean the foreground signals and recover an unbiased value of the tensor-to-scalar ratio whith an uncertainty compatible with LiteBIRD’s objectives. While we focused on the dust signal and the highest frequency bands of the instrument, we tested the robustness of our results under the addition of synchrotron as well as under various sky fractions and non zero input value for the tensor-to-scalar ratio.

In the subsequent paper Fuskeland et al (2023), I reused this pipeline to help demonstrating that having access to higher frequency bands allowed to ease the component separation by better characterizing the temperature complexity of the dust signal.

This component separation pipeline is still under devellopment and optimization in order to be applied to other scenarios of increasing generality and complexity. All my codes are available on this GitHub page.

Moreover, I am currently adding the moment coefficients in other already existing component separation methods, as fgbuster or commander in order to see if they can help tackling complex foreground scenarios.

I am also a member of the QUBIC collaboration, for which I project to use the moment expansion for component separation using the bolometric interferometry capabilities of the instrument.

Generalizing the moment expansion to polarization : the spin-moments

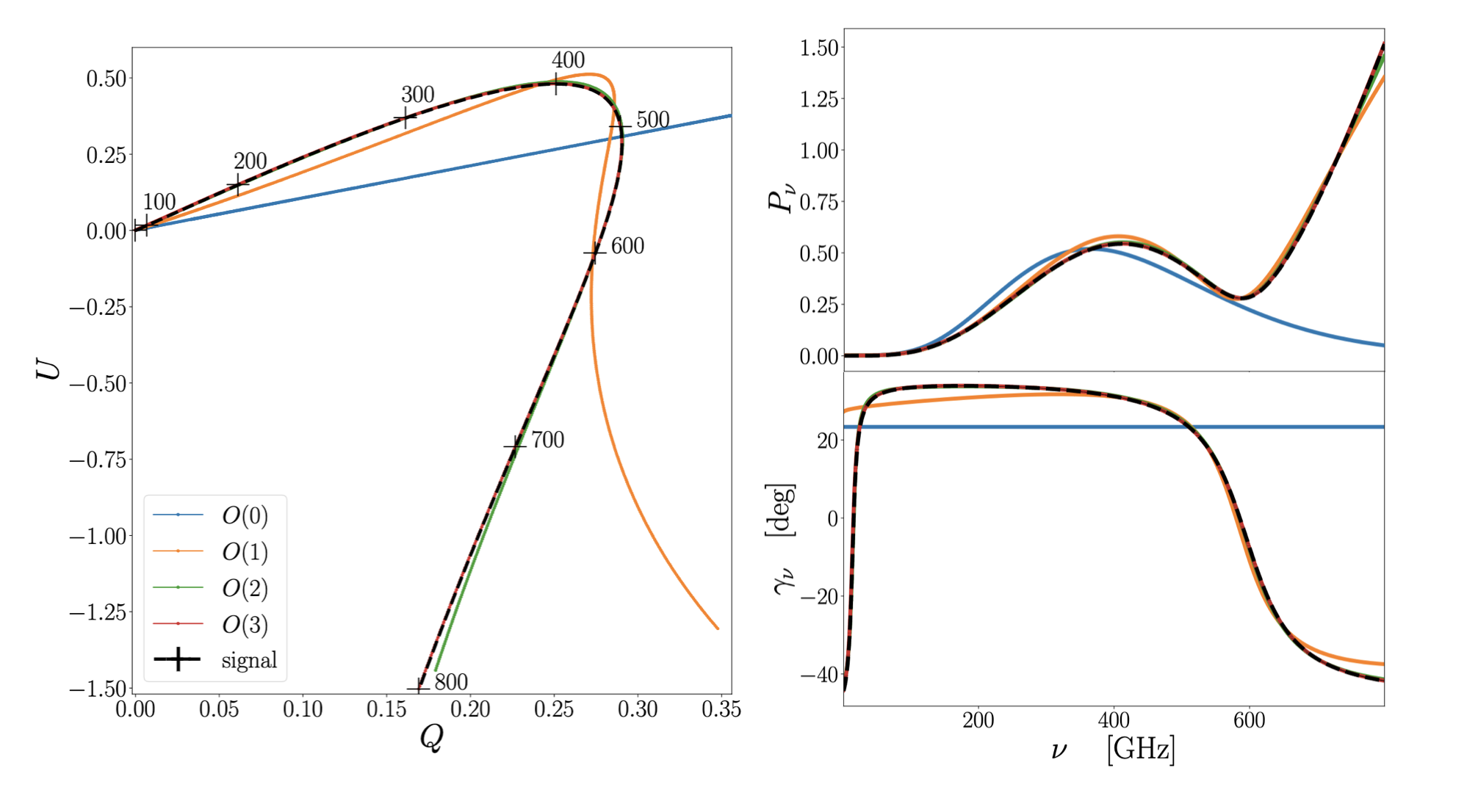
Modeling a distorted modified blackbody in the complex plane using the spin-moments at different orders (for explanations see Vacher et al (2023a)

The polarized signal present unique features as a prefered direction called the polarization angle. In the case of Galactic signal, the direction of the polarization angle is directly related to the orientation of the magnetic field in our Galaxy. In the presence of mixing, different polarization angles are also averaged, leading to complex phenomenon as a dependence with frequency of the total polarization angle. I name “polarized mixing” the averaging over emission points including both variations of the spectral parameters and of the polarization angles.

Willing to account for this rich and unique behavior, I provided the first consistent extension of the moment formalism to the polarization signal in Vacher et al (2023a).

To do so, I found that it was extremely convinient to model the polarized signal with the (spin-2) complex numbers $P=Q+iU$, where $Q$ and $U$ are the Stokes parameters. Propagating consistently the moment expansion in the complex plane, the moments are themselves promoted to complex numbers, called the “spin-moments”. This new formalism takes into account for the variations of the Galactic magnetic field and allows to model the spectral dependence of the total polarization angle.

In CMB science, it is common to use the $E$ and $B$ decomposition in order to analyze the polarized signal [Zaldariagga]. As such, I further extended the spin-moment formalism up to $E$- and $B$-modes level in Vacher et al (2023b). Doing so, I discovered that, in the presence of polarized mixing, $E$-modes should transform into $B$-modes and vice-versa, such that the $E/B$ ratio of foregrounds should be a frequency dependent quantity. I could verify that this behavior was observed in some toy-model filaments and in the foreground models used by the community. This helped us understand some of the results observed in Planck data (see next section). Moreover, I found that the three polarized angular power spectra $EE$, $BB$ and $EB$, must have different SEDs in the presence of mixing. This result is crucial for the study of cosmic birefringence, as it is not possible to infer safely the spectral behaviour of the unmeasured $EB$ spectra from the other spectra.

Using moment expansion for Galactic science

We further explored the moment expansion formalism to infer properties about the dust physics in Ritacco et al (2023). This paper was the first one to detect a different spectral behaviour for the $E$- and $B$-modes power spectra of the dust residuals in data, giving us a clew for the developments about $E/B$ discussed in the previous section. As a direct follow up, we are currently preparing another work targeting dust properties using the spin-moment formalism directly at the map level [Guillet et al (in prep)].

Scattering transform and more

Dust signal is not only complex is in the frequency space, but also in space. Indeed, due to the complex turbulent and magnetized behaviour of the interstellar medium, dust signal displays highly non Gaussian patterns over the sky, as filaments, drapery or clumps. I had the chance to investigates new statistics in order to tackle together the spatial and the spectral complexity of the foreground signal using scattering transform in Regaldo-Saint Blancard (2022). In this precursory work, we managed to infer some properties about the SED signal from the spatial non-Gaussian statistics of the signal only.

The $LiteBIRD$ instrument

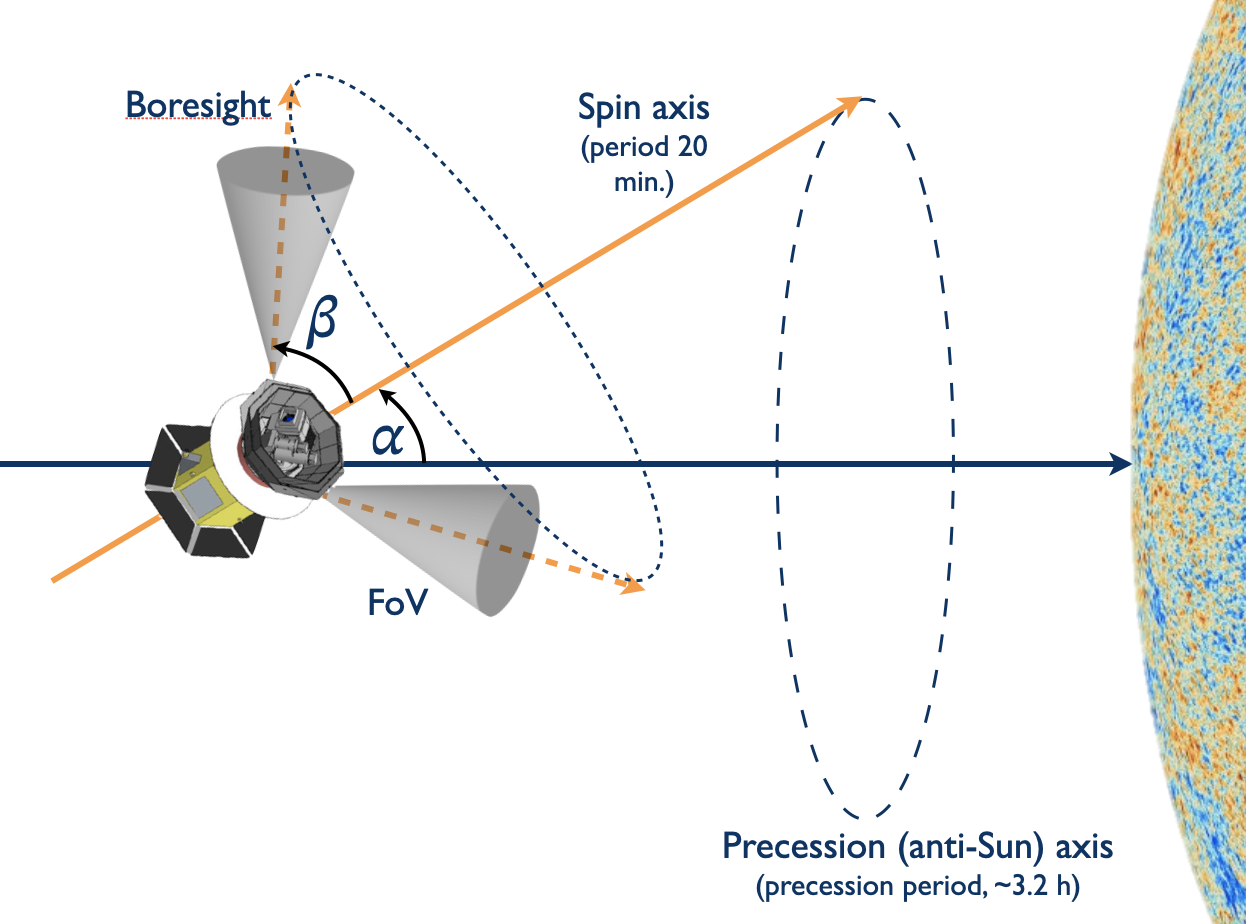
Definition of the scanning strategy of $LiteBID$ (for explanations see LiteBIRD Collaboration (2020))

I am strongly invested in the $LiteBIRD$ collaboration. Besides my main work on foregrounds and component separation described above, I also work on the study of the impact of some systematic effects on the observations. Specifically, I worked on optimizing the scanning strategy of the instrument in [Takase et al (in prep)]. In this work, we investigate how and at which space the $LiteBIRD$ satellite will have to rotate on himself in order to observe the sky in a way that ease as much as possible the final data analysis. $LiteBIRD$ will be rotating around the “L2” lagrange point, a point behind the moon, where the gravitational attraction of the sun and the one of the earth perfectly balance one another. No need to say that it will be impossible to go back there and tune it after the start of the mission, so choices like this must be carefully made now.

The Simons observatory

I just joined the collaboration. Hopefully, some of my contributions will appear here very soon!

Theories of gravity and fundamental constants

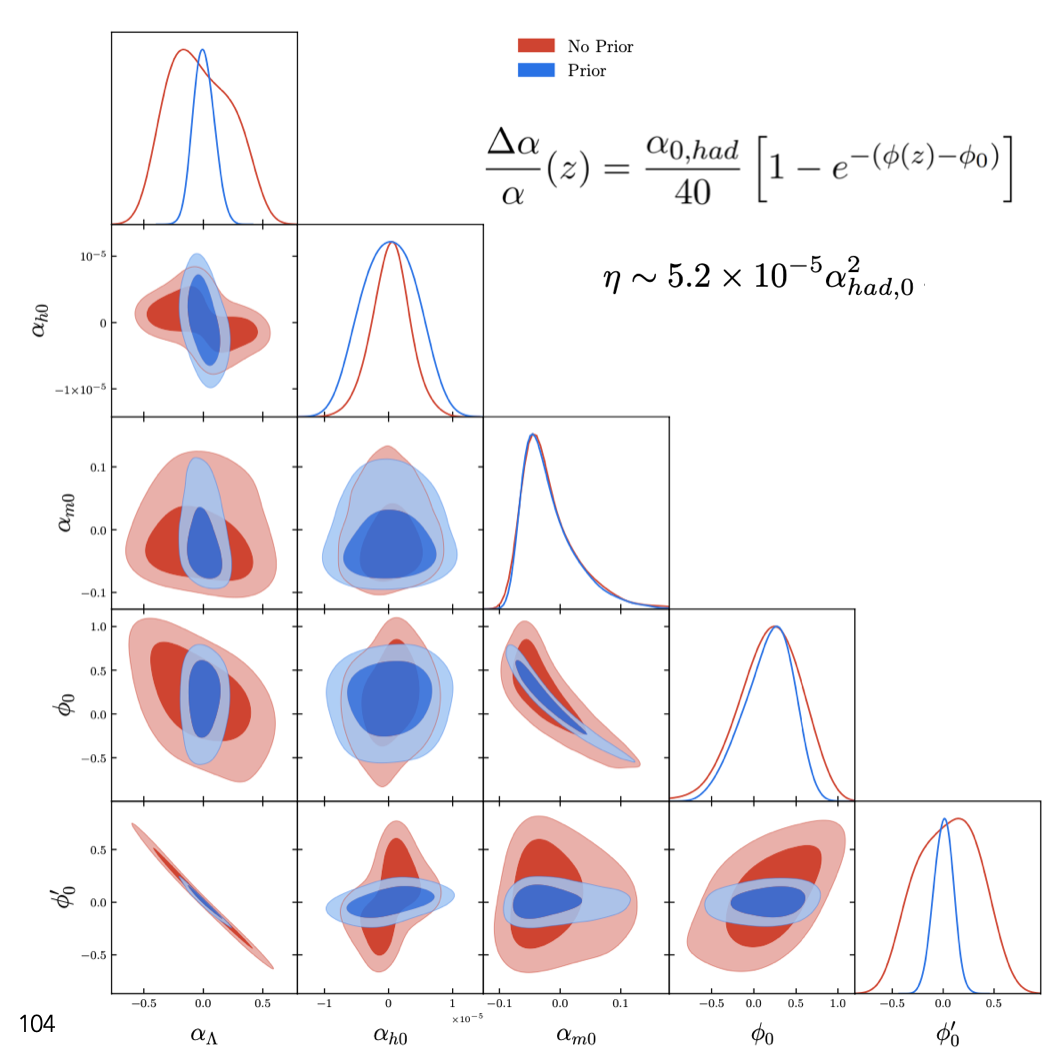
Constraints on one of the scenarios of the runaway dilaton model using Monte Carlo Markov Chains and synergy of multiple modern datasets (for explanations see Vacher et al (2023))

Constant variations and CMB

In direct connection with my work on CMB, I investigated the limits on building a coherent model in which variations of the fine structure constant during the recombination epoch could help solving the infamous $H_0$ tension Vacher and Schoneberg (2024).

Scalar fields and String theory

As part of my work since my first year of master’s internship in Porto (Portugal), I confronted some well motivated scalar field models expected to induce a space-time variation of the fundamental constants and a violation of the EEP (for more on this, see the dedicated section in my research interests).

I provided the latest to date constraints on the runaway dilaton model, inspired from string theory, first in Martins et Vacher (2019), using low redshift assumptions and in Vacher et al (2023), investigating the whole field evolution and using the latest datasets. We concluded that, facing the data, all the natural and expected values predicted by the models are excluded by current measurements, such that string theory – in which the dilaton is an uncircumventable prediction – is significantly challenged and will have to explain such a stability of the fundamental constants.

I did a similar exploration of the so called Bekenstein models, in Vacher et al (2022), in which I investigate various different scenarios. Here again, all the natural values motivated from high energy physics appear to be excluded by data.

Finally, in Schöneberg et al (2023), we investigated the so-called string Swampland conjecture, in regards with the cosmological latest datasets, using considerations about varying constant models. We stressed that, beside the violation of the Swampland conjectures, the observed stability of the fundamental constant and non violation of the EEP shrinks further the viability domain of the possible scalar field extensions of the standard models.

Using Euclid to probe gravity

I am also a member of the Euclid consortium, in which I investigate how this large cosmological survey can be used to probe the possible variations of the fundamental constants. In particular, we investigate how a varying fine structure constant can impact Euclid’s observables as the matter power spectrum. Our results will be published soon in a collaboration paper [Euclid collaboration (in prep)].